推奨のテーブルの送り速度はありますが、面粗度との関係が書いていなかったので、関係を整理しました。
荒加工と仕上げの時の条件の違いは?
下記の通り、フライスの加工時間を計算することができたのですが、荒加工と仕上げの際の条件の違いに言及されておらず、切削速度(≒回転数)、一刃当たりの送りを考えたらいいのかわからない状態になってしまいました。そこで、いろいろと検索したところ、一刃当たりの送りが面粗度に大きく影響してくることが分かりましたので、今回紹介していこうと思います。
面粗度=一刃当たりの送りで決まる。
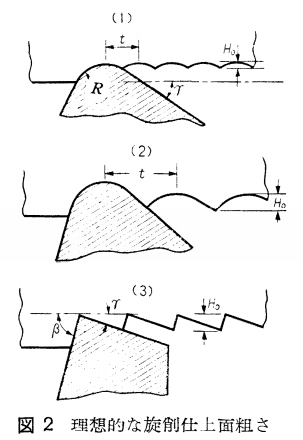
下記の図をご覧ください。
下の図では「t」が一刃当たりの送り、段差H0が面粗度を表しております。
ですので、tを無限に小さくし、段差がつかないようにすれば理論上面粗度が0になることが分かります。
このように、一刃当たりの送りが面粗度に非常に聞いてくるのです。
では、実際に計算で求めていきましょう。
(1)丸みを帯びている場合
Ra=3.2μm ノーズR=0.2mm の計算
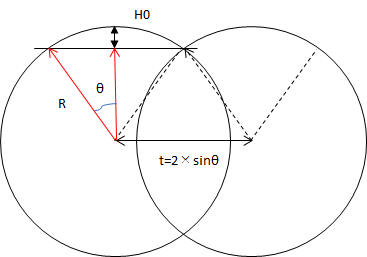
tとRとH0の関係を図に表すと下記のような関係になる。
cosθ=(R-H0)/Rであり、t=2×Rsinθとなることが分かる。
よって、t=2×Rsin(acos(R-H0)/R) で求めることができる。
ここで、Raの4倍をRz=H0とすると、H0=Ra*4/1000。
よって、t=2×Rsin(acos(R-Ra*4/1000)/Rとなる
今回の値を代入していくと、
t=2×0.2×sin(acos(0.2-3.2*4/1000)/0.2) acos(0.2-3.2*4/1000)/0.2=20.6°
t=2×0.2×sin20.6°= 2×0.2×0.352 ≒ 0.14 となる。
(3)丸みを帯びていない場合
丸みを帯びていない場合、同じように計算していくと、
t=Ra×4/1000 ×{(tanβ*tamγ)/(tanβ+tanγ)}となる。
正三角形のチップで90°の傾きの時、β=γ=45°になるので、Ra=3.2とすると
t=3.2×4/1000×(1*1)/(1+1)=0.006と非常に細かい送り速度が必要になってくる。
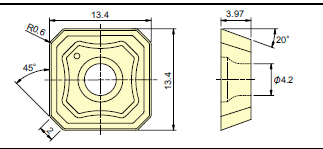
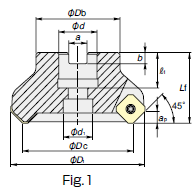
カタログから算出してみる
カタログから算出してみようとしたところ、なんと、、もとから2mmの幅で削られる設定になっており、工具が摩耗しない限り、最大2mmの送りで切削していっても粗さは理論的には0になるインサートチップとなっていた。ちなみに、この時の推奨の一刃当たりの送りは0.2mmとなっており、十分クリアできるレベルとなっている。なので、
結果 理論粗さは一刃当たりの送りで計算できる。
今回分かったことは少々複雑ではあるが、一刃当たりの送りを調整することで面粗度をコントロールすることができることが分かった。切削速度に関しては、工具の寿命に大きくかかわってくるため、スピードを上げることができないが、送りに関しては工具の寿命に大きく影響を与えないことが分かっているので、必要最低限の面粗度を確保しつつ、送り速度を上げていくことが望ましいと考える。




コメント欄